Data Structure - Graph Data Structure - Learnengineeringforu

A graph is pictorial representation of a set of objects where some pairs of objects are cnnects by links. The interconnected objects are represented by points termed as Vertices, and the links that connect the vertices are called edges.

Formally, a graph is a pair of sets (V,E),Where V is the et of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph -

                                                
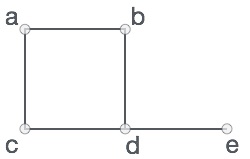
In the above graph,
V={a, b, c, d, e}
E={ab, ac, bd, cd, de}

Graph Data Structure

Mathematical graphs can be represented in data structure. We can represent a graph using an array of vertices and a two-dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms −

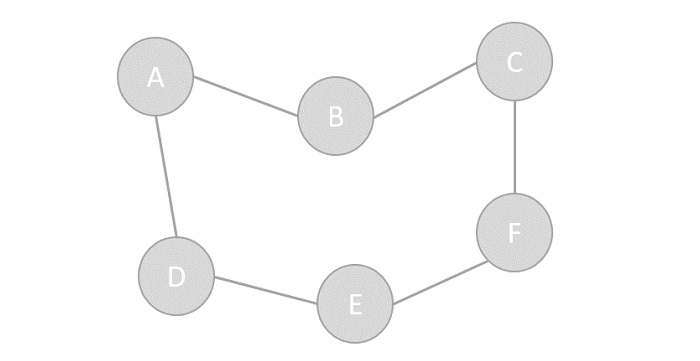
• Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
• Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
• Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
• Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D. 
•                             

Basic Operations

Following are basic primary operations of a Graph -

• Add Vertex − Adds a vertex to the graph.
• Add Edge − Adds an edge between the two vertices of the graph.
• Display Vertex − Displays a vertex of the graph.
• 
  

This article is contributed by Khan Shadab Alam. If you like Learnengneeringforu and would like to contribute, you can also write an article for our learnenrs.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.